The Ship, the Shore and the Philosopher
- Jane Orton

- May 2, 2022
- 5 min read
Updated: Jul 21, 2025
Dr. Orton investigates the geometrical heist that stole our fate back from the gods.

In the time of Homer, the Greeks were at the mercy of the gods. Promethius was punished horribly by Zeus for stealing fire from the gods to give to humanity in the form of technology, science and civilisation. He was bound in chains while an eagle pecked out his liver, only to experience the same torment again, as the liver regrew every day. The gods were not champions of human empowerment.
During the fifth and sixth centuries, though, things in the Mediterranean were changing. Some scholars describe this as a transition from μῦθος to λόγος: a turning away from mythos (myth), towards logos (reason). Rather than being at the mercy of the whims of the gods, people could begin to see patterns in the way the world works, and to use these patterns as a way to control their own fate. The earliest known participant in this trend, Thales of Miletus, learned geometry from the Egyptians and began to apply it to the practical issues of the Ancient World.
Thales was a mathematical troubleshooter. There was a rumour going around the ancient Mediterranean that he enabled an army to cross the Halys river by diverting a part of it and he is also said to have mapped out the stars of Ursa Minor, which the Phoenicians used to sail. Known as the first Greek mathematician, Thales was also said to be the first to predict eclipses and to fix solstices. With Thales around, there was no need to look to the gods for an explanation.
Gazing out over the balmy Mediterranean sea, Thales was able to work out how far a ship was from the shore using the properties of triangles later set out in Euclid I.26:
If two triangles have the two angles equal to two angles respectively, and one side equal to one side, namely, either side adjoining the equal angles, or that subtending one of the equal angles, they will also have the remaining sides equal to the remaining sides and the remaining angle to the remaining angle.
For the detective of mathematical history, however, there is a mystery to solve. We only know that Thales used these principles from the Eudemian Summary written by Proclus in the fifth century – hundreds of years after both Thales and Euclid. Proclus tells us that Eudemus attributes the theorem to Thales on the grounds that his method “must have made use of it,” but it is not clear that Thales needs the concept of proof that is found in Euclid: he may simply assume the truth of the rules about triangles that this embodies, without having to know how it is that they are true.
Eudemus precedes Euclid, so the summary cannot have been written by Eudemus as it stands, and perhaps not even by Proclus. It is possible that Eudemus does attribute to Thales the use of that method, and the author of the summary merely cross references this theory with Euclid 1.26. In fact, Eudemus does make attributions to Thales in his History of Astronomy, which does suggest that Eudemus does attribute the practical application of certain mathematical rules to Thales. How exactly did Thales work it out?
Given that we cannot use Pythagoras’ theorem as it was a later discovery, the most geometrically straightforward method that Thales could have used is as follows:
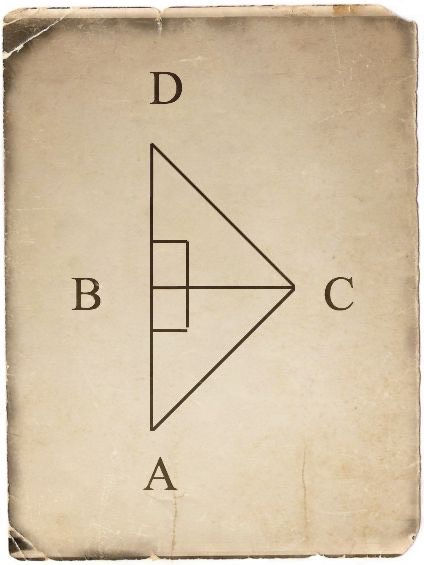
Thales stands at B, the shore, and wishes to know the distance to the ship at D. He picks another point on the shore, C, and measures the distance BC and the angle BCD. He then measures an equal angle, BCA to create line CA, which intersects the extension of DB at point A. The distance AB is equal to BD.
The problem with this is that it seems impractical as a method of calculating the distance of a ship from the shore: if the ship were very far out, Thales would need a large extent of level ground to measure AC and BA. Though it seems reasonable geometrically, the impracticality of this method means that we should reject it. We wish to find a solution that is practical, as well as being mathematically sound. Moritz Cantor proposes the following solution:
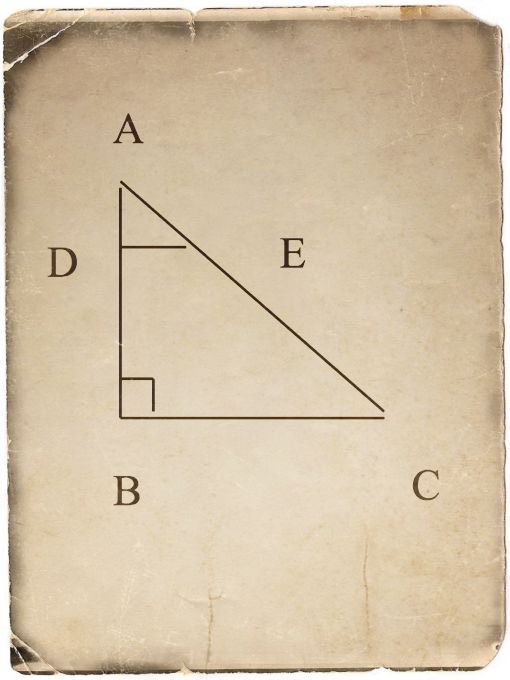
Thales stands on a tower at A with a right angle-shaped instrument. The small right angled triangle ADE has common angles to ABC, so the length of BC can be determined by DE by proportion. This does not require the use of much level ground.
As Thomas Heath points out, this effectively resorts to the use of similar triangles, as opposed to reconstructing the same triangle somewhere else and measuring it: if Thales had used this method, it is more likely that Proclus would have mentioned Euclid VI.4, rather than I.26. For the sake of mathematical coherence and practical considerations, we have strayed rather far from the evidence.
Heath proposes the following solution:
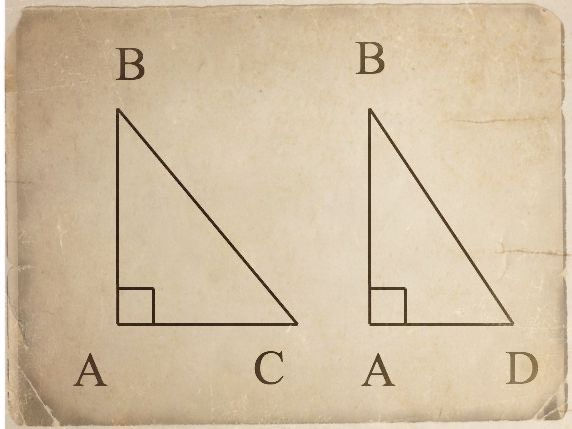
Thales stands on the tower at B with a stick and cross-piece to fix an angle. He fixes the stick upright and directs the crosspiece at the ship. He fixes the crosspiece at this angle, ABC. He creates triangle ABD, where D is the point on the shore determined by angle ABD being the same as ABC .The distance AD=AC, the distance of the ship from the shore.
This method has the advantage of requiring the kind of knowledge needed for Euclid I.26 – triangles ABC and ABD share two angles and a corresponding side – and it also means that Thales could choose where to construct the second triangle, if there were some obstructions.
Thales needs some knowledge of the properties of triangles, most likely assuming the truth of Euclid I.26, without necessarily having to prove it. Rather than having an abstract notion of proofs, he may take a more empirical approach: from what he sees of triangles, he generalises that all triangles with two angles and a corresponding side the same are equal, so the probability is that this was true for all triangles. Even before we had access to the proofs of Euclid, Thales was using knowledge previously reserved for the gods to help humanity shape our own fate.
Find Out More
Follow our Classics blog series for more articles about the ancient world and listen to Dr. Orton’s academic lectures on the history and philosophy of the Ancient World on our Research Page.
If you’re interested in tutorials with Dr. Orton, she offers online, one-on-one tutorials that are based around your learning or research needs. This ranges from ad hoc tutorials to gain an understanding of the academic literature, research proposal feedback and development, or regular, ongoing support. Take a look at our Philosophy course on Ancient Philosophy. Those who like a good historical mystery or mathematicians wanting to know more about the history of their discipline might also enjoy our Classics course on Mathematics and Philosophy in the Ancient World. Lean about the antics of the gods in our courses on Homer and Virgil, or in our course on Greek Religion.
These are templates of possible routes of study and can be combined, adapted, or designed from scratch to suit your interests and goals. Dr. Orton will work with you to design a course of private tutorials tailored to your needs, ability and schedule – whether you are undertaking your own research for an independent project, writing a book or simply have a personal interest. Click the link to find out what it’s like to work with her!
Contact us to find out more and follow us on Orton Academy Instagram to see pictures from Dr. Orton’s fieldwork in the Himalayas and the Sundarbans – we would love to connect with you!




Comments